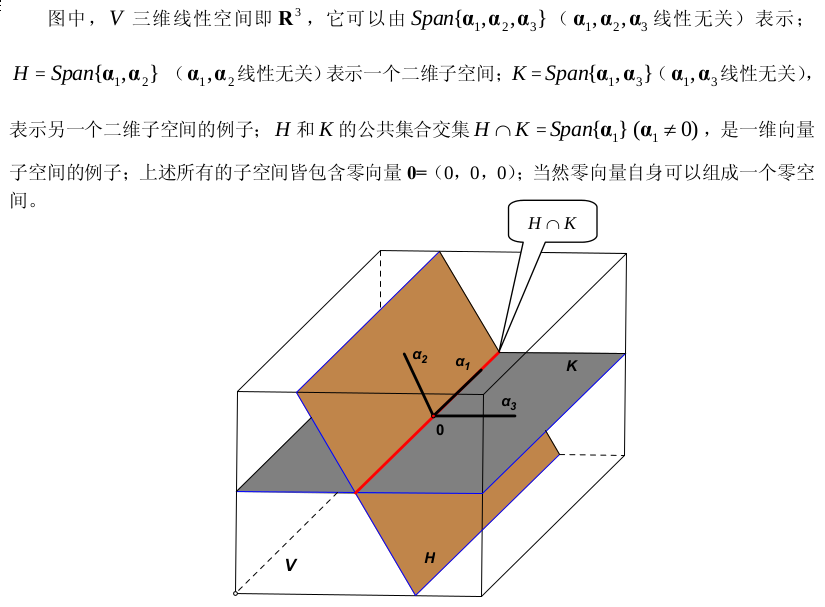
向量组和向量空间

向量的线性表示和组合的几何意义

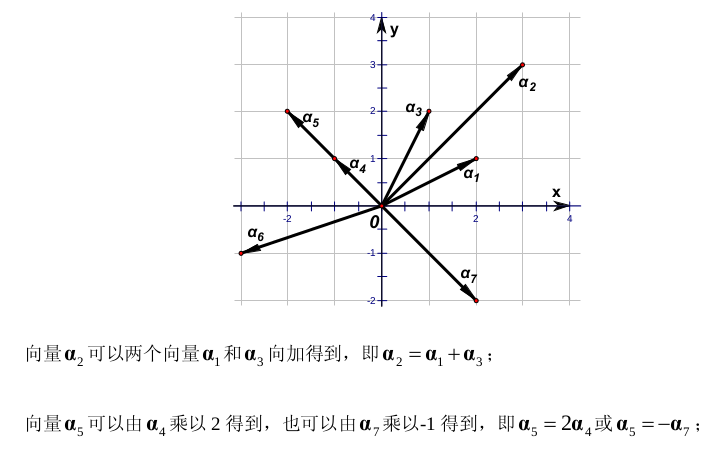
向量的线性相关和线性无关的几何意义

向量组的秩及极大无关向量组

从几何意义上讲,在一个向量组里,如果有多个向量在一条直线上,哪么这些向量只要一个向量就可以了, 其他的同直线的向量可以被代表了。这个向量代表可以是任意一个非零向量;进而,如果向量组里还有多 个向量构成且存在于一个平面上,那么只要有两个非零非共线的向量就可以代表其他的共面向量了;继续, 如果向量组里还有多个向量构成且存在于一个立体空间里,那么只要有三个非零非共线非共面的向量就可 以代表其它的同立体向量了...。

• 使用向量空间的概念,我们可以有一个更全面的关于线性相关的几何意义的结论:
  • 一个向量空间中,一个向量组线性相关的话,那么这个向量组中全部向量会属于一个子向量空间中,且子空间的维数要小于向量组元素的个数;
  • 一个向量空间中,一个向量组线性无关的话,那么这个向量组中全部向量会属于一个子向量空间中,且子空间的维数要大于或等于向量组元素的个数;

上面两句话意思就是说,一个向量组应该可以张成一个和向量组元素个数相同的子空间,一个 向量张成一维的子空间,两个向量应张成二维的字空间...;如果一个向量组n个元素,张成一个 小于n的子空间,那么这个向量组就线性相关;如果总是张成一个n维的子空间,那么这个向量组 就线性无关。

• 线性相关或无关的向量组的秩就是可以张成的最大子空间的维数;
• 两个向量组等价,就是两个向量组张成的向量子空间相同或重合;

向量空间的几何意义

• 设一个向量组 {α1 , α 2 ...α n } ,这个向量组的所有的线性组合生成一个向量集合:

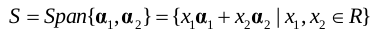
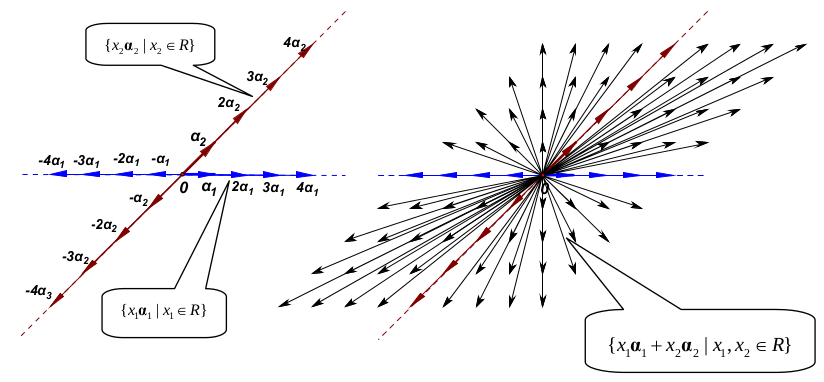
子空间的几何意义